[最も欲しかった] 体積 表面積 関係 123553
+%EF%BC%91+%EF%BC%92+%C3%97%EF%BC%94%C3%97%EF%BC%93%EF%BC%9D%EF%BC%96+%EF%BC%91%EF%BC%92%C3%97%EF%BC%92%EF%BC%8B%EF%BC%97%EF%BC%92%EF%BC%9D%EF%BC%98%EF%BC%94+(%E3%8E%9D2)+%EF%BC%95%E3%8E%9D+%EF%BC%96%E3%8E%9D.jpg "側 面積 の 求め 方 円錐の表面積 簡単な求め方とその理由を解説するぞ 中学数学 理科の学習まとめサイト")
側 面積 の 求め 方 円錐の表面積 簡単な求め方とその理由を解説するぞ 中学数学 理科の学習まとめサイト
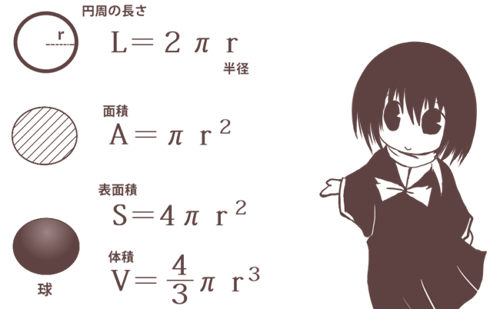
※ 球の表面積 S は円の面積 πr 2 の4倍になる．（非常にきれいな関係） ※ 高校数学IIIで微分を習えば，体積 を半径で微分すると表面積 S=4πr 2 になることが分かる．脱線ついでに言えば，円の面積 S=πr 2 を半径で微分すると円周の長さ L=2πr になる．球の体積と表面積について 新潟県立阿賀黎明高等学校 西條和久 平成14年11月29日 1 はじめに 来年度より，新学習指導要領が実施され，いくつかの中学校の内容が高校へ移行する。
体積 表面積 関係
体積 表面積 関係-＞━━━━━━━━━━━━━━━━＜ 動画まとめシートを配布中！ 《 林俊介の公式LINE球の体積や表面積と、その球がちょうど入る円柱の体積や側面積との関係を、計算結果等で 確かめ、イメージとしてもっておきましょう。 2（ 1 ）球の表面積を求める公式： S＝4πr2 （ 2）円柱の底面の円の半径： r ，円柱の高さ： 2r （
3
位置関係2 直線の位置関係／面と直線の位置関係／角柱・角錐の体積／立体の切断など／ 円柱と円錐の体積 ／円柱と円錐の表面積／球の体積・表面積／展開図／投影図／ FdData 入試製品版のご案内 FdData 入試ホームページ 体積と表面積の関係で質問があります．たとえば，球は体積 4πr^3/3 を r について微分したものが表面積になりますが，一般的な立体についてはどうなのでしょうか？一般的な立体について，体積と表面積には何らかの関係があるのでしょうか表面積：体積とその熱との関係 生物学では、より広い表面積とより少ない体積が体を冷たく保つのに役立つと述べられています。 この現象を物理学的にどのように説明できるでしょうか。 ごめんなさい。 かっこいい。 表面積が大きいほど、体から出る
半径 r の球の表面積を求めよ。 解答 例5 例1の直円錐の表面積を区間0,rで求めよ。 解答 なお、体積Vは、V＝1/3πr 3 例6 y＝f(x)＝r として例2にならい直円柱の表面積を区間0,lで求めよ。 解答 なお、体積Vは、V＝πr 2 l 表面積は 2(abbcca)r^2 で、これと一致しません。 球の場合に、体積を拡大率で微分すると表面積になるのは、 球面が接平面で非常によく近似できて、厚さがどこでも一様 半径がわずかに異なる二つの球の体積の差が、球面積×半径無料でダウンロード・プリントアウトできる小学生用・算数の単位換算表 です。 小学校で習う、時間、長さ、かさ、重さ、面積、体積の単位の一覧、早見表を作ってみました。 関連ページ ⇒小学6年生 いろいろな単位・単位の計算 問題プリント
体積 表面積 関係のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
 微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
 微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
「体積 表面積 関係」の画像ギャラリー、詳細は各画像をクリックしてください。
微分積分学 11回目 |  微分積分学 11回目 | 微分積分学 11回目 |
 微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
 微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
「体積 表面積 関係」の画像ギャラリー、詳細は各画像をクリックしてください。
 微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
 微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
「体積 表面積 関係」の画像ギャラリー、詳細は各画像をクリックしてください。
微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
 微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
 微分積分学 11回目 |  微分積分学 11回目 | 微分積分学 11回目 |
「体積 表面積 関係」の画像ギャラリー、詳細は各画像をクリックしてください。
微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
微分積分学 11回目 |  微分積分学 11回目 | 微分積分学 11回目 |
 微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
「体積 表面積 関係」の画像ギャラリー、詳細は各画像をクリックしてください。
 微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
 微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
 微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
「体積 表面積 関係」の画像ギャラリー、詳細は各画像をクリックしてください。
 微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
 微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
 微分積分学 11回目 | 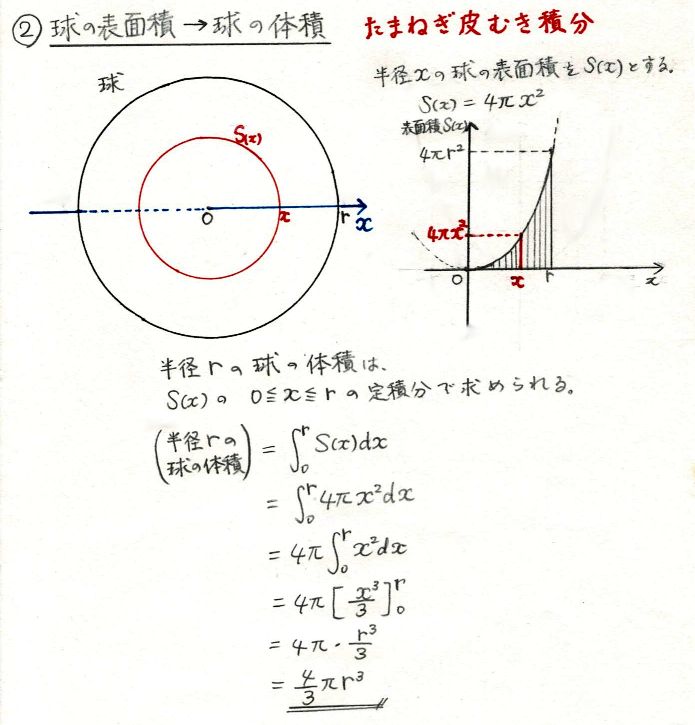 微分積分学 11回目 |  微分積分学 11回目 |
「体積 表面積 関係」の画像ギャラリー、詳細は各画像をクリックしてください。
微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
 微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
 微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
「体積 表面積 関係」の画像ギャラリー、詳細は各画像をクリックしてください。
 微分積分学 11回目 | 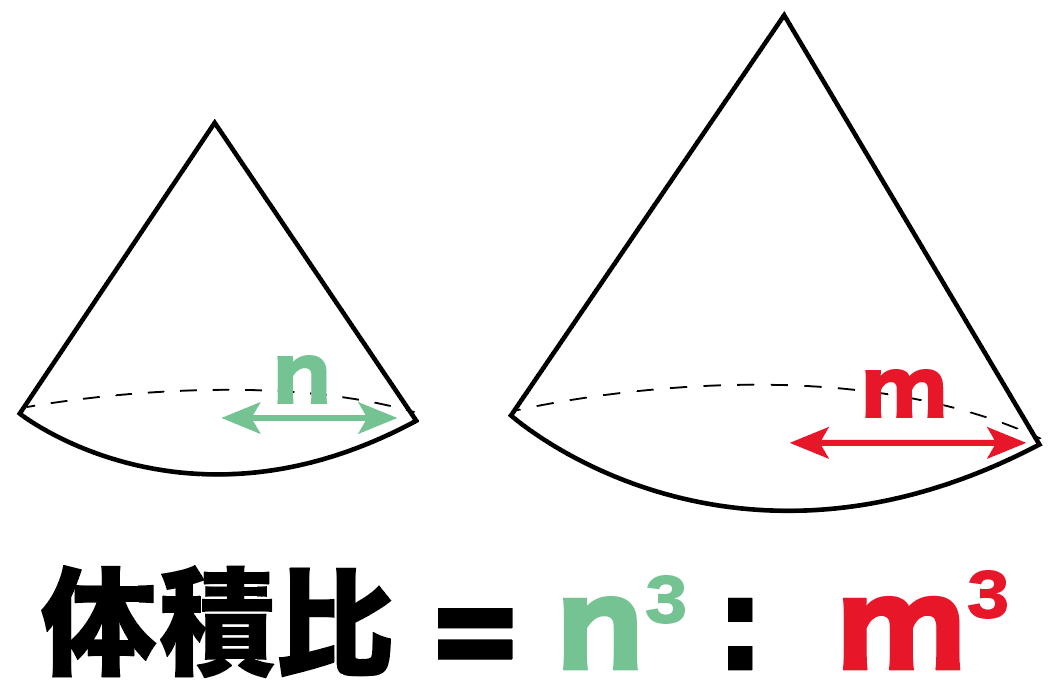 微分積分学 11回目 |  微分積分学 11回目 |
 微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
 微分積分学 11回目 | 微分積分学 11回目 |  微分積分学 11回目 |
「体積 表面積 関係」の画像ギャラリー、詳細は各画像をクリックしてください。
 微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
 微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
 微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
「体積 表面積 関係」の画像ギャラリー、詳細は各画像をクリックしてください。
 微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
 微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
 微分積分学 11回目 |  微分積分学 11回目 |  微分積分学 11回目 |
「体積 表面積 関係」の画像ギャラリー、詳細は各画像をクリックしてください。
 微分積分学 11回目 |  微分積分学 11回目 | 微分積分学 11回目 |
 微分積分学 11回目 |  微分積分学 11回目 |
※ 球の表面積は円の面積の4倍になる．（非常にきれいな関係） ※ 高校数学IIIで微分を習えば，体積 V= πr 3 を半径で微分すると表面積 S=4πr 2 になることが分かる．脱線ついでに言えば，円の面積 S=πr 2 を半径で微分すると円周の長さ L=2πr になる． 相似比と表面積と体積の関係 相似な図形が2つあり、相似比がa：bならば、表面積比は a²：b² 、体積比は a³：b³ になります。 注意：相似な図形である場合に限ります。
コメント
コメントを投稿